2015年全国研究生数学建模竞赛A题
水面舰艇编队防空和信息化战争评估模型
我海军由1艘导弹驱逐舰和4艘导弹护卫舰组成水面舰艇编队在我南海某开阔海域巡逻,其中导弹驱逐舰为指挥舰,重要性最大。某一时刻t我指挥舰位置位于北纬15度41分7秒,东经112度42分10秒,编队航向200度(以正北为0度,顺时针方向),航速16节(即每小时16海里)。编队各舰上防空导弹型号相同,数量充足,水平最小射程为10千米,最大射程为80千米,高度影响不必考虑(因敌方导弹超低空来袭),平均速度2.4马赫(即音速340米/秒的2.4倍)。编队仅依靠自身雷达对空中目标进行探测,但有数据链,所以编队中任意一艘舰发现目标,其余舰都可以共享信息,并由指挥舰统一指挥各舰进行防御。
以我指挥舰为原点的20度至220度扇面内,等可能的有导弹来袭。来袭导弹的飞行速度0.9马赫,射程230千米,航程近似为直线,一般在离目标30千米时来袭导弹启动末制导雷达,其探测距离为30千米,搜索扇面为30度(即来袭导弹飞行方向向左和向右各15度的扇面内,若指挥舰在扇形内,则认为来袭导弹自动捕捉的目标就是指挥舰),且具有“二次捕捉”能力(即第一个目标丢失后可继续向前飞行,假设来袭导弹接近舰艇时受到电子干扰丢失目标的概率为85%,并搜索和攻击下一个目标,“二次捕捉”的范围是从第一个目标估计位置算起,向前飞行10千米,若仍然没有找到目标,则自动坠海)。每批来袭导弹的数量小于等于4枚(即由同一架或在一起的一批飞机几乎同时发射,攻击目标和导弹航向都相同的导弹称为一批)。
由于来袭导弹一般采用超低空飞行和地球曲率的原因,各舰发现来袭导弹的随机变量都服从均匀分布,均匀分布的范围是导弹与该舰之间距离在20-30千米。可以根据发现来袭导弹时的航向航速推算其不同时刻的位置,故不考虑雷达发现目标后可能的目标“丢失”。编队发现来袭导弹时由指挥舰统一指挥编队内任一舰发射防空导弹进行拦截,进行拦截的准备时间(含发射)均为7秒,拦截的路径为最快相遇。各舰在一次拦截任务中,不能接受对另一批来袭导弹的拦截任务,只有在本次拦截任务完成后,才可以执行下一个拦截任务。指挥舰对拦截任务的分配原则是,对每批来袭导弹只使用一艘舰进行拦截,且无论该次拦截成功与否,不对该批来袭导弹进行第二次拦截。不考虑每次拦截使用的防空导弹数量。
请通过建立数学模型,解决以下几个问题:
一, 在未发现敌方目标时,设计编队最佳队形(各护卫舰相对指挥舰的方位和距离),应对所有可能的突发事件,保护好指挥舰,使其尽可能免遭敌导弹攻击。
二, 当不考虑使用电子干扰和近程火炮(包括密集阵火炮)等拦截手段,仅使用防空导弹拦截来袭导弹,上述编队防御敌来袭导弹对我指挥舰攻击时的抗饱和攻击能力如何(当指挥舰遭遇多批次导弹几乎同时攻击时,在最危险的方向上,编队能够拦截来袭导弹的最大批数。)?
三, 如果编队得到空中预警机的信息支援,对距离我指挥舰200千米内的所有来袭导弹都可以准确预警(即通报来袭导弹的位置与速度矢量),编队仍然保持上面设计的队形,仅使用防空导弹拦截敌来袭导弹对我指挥舰攻击时的抗饱和攻击能力(定义同上)提高多少?
四, 预警机发现前方有12批可疑的空中目标,从t时刻起,雷达测得的目标位置信息在附件1的表格中(说明:表中作战时间为time_t格式,即从1970年1月1日0时起到某一时刻的秒数;目标位置经纬度的单位为弧度;目标高度的单位为米),各目标雷达反射面积见表1。用于判断空中目标的意图的知识和规则的样本见表2。请分析识别空中各目标可能的意图。(相关的背景知识介绍参见附件A)
五, 如果我方的预警机和水面舰艇编队的雷达和通信系统遭到敌方强烈的电子干扰,无法发现目标,也无法传递信息,这时,后果将是极其严重的,我编队防空导弹的拦截效能几乎降低到零。由此引起人们的深思,信息化条件下作战对传统的作战评估模型和作战结果已经产生重要的甚至某种程度上是决定性的影响!在海湾战争(相关资料参见附件B)的“沙漠风暴”行动开始前,一些军事专家用传统的战争理论和战争评估模型进行预测,包括用兰彻斯特战争模型预测战争进程,结果却大相径庭,战争的实际结果让他们大跌“眼镜”。那么信息化战争的结果应该用什么样的模型来分析或预测呢?这是一个极具挑战性,又十分有意义的课题。请尝试建立宏观的战略级信息化战争评估模型,从一般意义上反映信息化战争的规律和特点,利用模型分析研究信息系统、指挥对抗、信息优势、信息系统稳定性,以及其它信息化条件下作战致胜因素的相互关系和影响(信息化战争相关概念参见附件C)。并通过信息化战争的经典案例,例如著名的海湾战争,对模型加以验证。
表1 空中目标的雷达反射面积
| 目标ID |
雷达反射面积(m2) |
| 41006893 |
3.1 |
| 41006830 |
3.5 |
| 41006831 |
5.7 |
| 41006836 |
1.9 |
| 41006837 |
4.3 |
| 41006839 |
5.5 |
| 41006842 |
2.6 |
| 41006851 |
5.5 |
| 41006860 |
6.2 |
| 41006872 |
1.7 |
| 41006885 |
1.1 |
| 41006891 |
3.6 |
表2 已知意图的15批空中目标数据
| 空中目标 |
方位角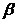 (mil) (mil) |
距离 (km) (km) |
水平速度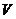 (m/s) (m/s) |
航向角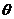 (°) (°) |
高度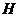 (km) (km) |
雷达反射面积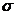 (m2) (m2) |
目标属性 |
意图 |
| 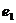
|
810 |
281 |
250 |
202 |
6.0 |
3.0 |
中目标 |
侦察 |
| 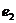
|
2 300 |
210 |
300 |
310 |
4.0 |
1.2 |
小目标 |
攻击 |
| 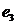
|
820 |
280 |
245 |
201 |
6.5 |
5.4 |
大目标 |
侦察 |
| 
|
2 325 |
215 |
320 |
324 |
4.2 |
2.8 |
中目标 |
攻击 |
| 
|
830 |
282 |
255 |
200 |
4.2 |
4.7 |
大目标 |
侦察 |
| 
|
825 |
284 |
250 |
204 |
5.0 |
2.6 |
中目标 |
侦察 |
| 
|
2 250 |
150 |
300 |
155 |
5.0 |
3.3 |
中目标 |
攻击 |
| 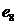
|
4 000 |
110 |
300 |
50 |
3.4 |
2.1 |
中目标 |
掩护 |
| 
|
2 800 |
260 |
215 |
260 |
7.7 |
6.8 |
大目标 |
监视 |
| 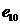
|
5120 |
110 |
210 |
52 |
3.6 |
3.7 |
中目标 |
其它 |
| 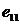
|
4 020 |
120 |
280 |
52 |
3.6 |
1.7 |
小目标 |
掩护 |
| 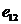
|
4800 |
140 |
220 |
18 |
9.6 |
5.7 |
大目标 |
其它 |
| 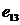
|
480 |
295 |
292 |
245 |
9.9 |
6.9 |
大目标 |
其它 |
| 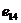
|
2 450 |
210 |
230 |
210 |
5.0 |
1.2 |
小目标 |
其它 |
| 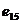
|
2900 |
290 |
272 |
350 |
5.6 |
5.2 |
大目标 |
攻击 |
| |
|
|
|
|
|
|
|
|
说明:
1、方位角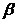 (mil)是指从我指挥舰到空中目标方向的方位角:正北时
(mil)是指从我指挥舰到空中目标方向的方位角:正北时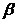 =0,顺时针方向一周分为6400mil
=0,顺时针方向一周分为6400mil
2、距离 (km)是指从我指挥舰位置到空中目标的距离;
(km)是指从我指挥舰位置到空中目标的距离;
3、水平速度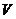 (m·s-1)是指空中目标在水平面上的速度;
(m·s-1)是指空中目标在水平面上的速度;
4、航向角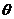 (°)是指空中目标飞行的方向(正北为0度,顺时针方向一周分为360度);
(°)是指空中目标飞行的方向(正北为0度,顺时针方向一周分为360度);
5、高度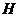 (km)是指空中目标距海平面的垂直距离;
(km)是指空中目标距海平面的垂直距离;
6、雷达反射面积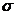 (m2)是指目标在雷达上回波的大小:0≤
(m2)是指目标在雷达上回波的大小:0≤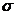 <2为小目标,2≤
<2为小目标,2≤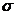 <4为中目标,
<4为中目标,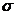 ≥4为大目标。
≥4为大目标。
参考文献
1.姜启源. 数学模型[M]. 高等教育出版社. 1993.
2.胡晓峰. 战争复杂系统建模与仿真[M].北京:国防大学出版社.2005.
3. 张为民. 作战仿真建模理论与方法[M].北京:海潮出版社.2009.
4. 军事科学院军事历史研究部. 海湾战争全史[M].北京:解放军出版社.2000.12
5. 张啸天等. 多维战争中兰彻斯特方程探讨[M].火力与指挥控制.2008. 33(2)
6. 孔红山等. 兰彻斯特方程的系统动力学模型研究[M].计算机工程与设计.2011. 32(8)
7. 史彦斌等. 基于兰彻斯特方程的信息支援效能研究[M].航空计算技术.2007. 37(5)
8. 唐铁军, 徐浩军.应用兰彻斯特法进行体系对抗效能评估[M].火力与指挥控制.2007. 32(8)


