2016第八届大学生数学竞赛试卷(非数学类)
一、填空题(每小题5分,满分30分)
1、若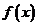 在点
在点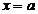 可导,且
可导,且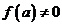 ,则
,则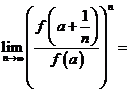 .
.
2、若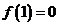 ,
,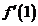 存在,求极限
存在,求极限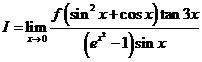 .
.
3、设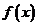 有连续导数,且
有连续导数,且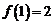 ,记
,记 ,若
,若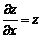 ,求
,求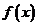 在
在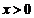 的表达式.
的表达式.
4、设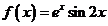 ,求
,求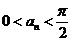 ,
,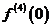 .
.
5、求曲面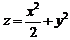 平行于平面
平行于平面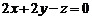 的切平面方程.
的切平面方程.
二、(14分)设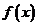 在
在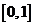 上可导,
上可导,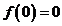 ,且当
,且当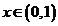 ,
,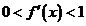 ,
,
试证当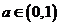 ,
,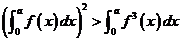 .
.
三、(14分)某物体所在的空间区域为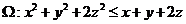 ,密度函数为
,密度函数为 ,求质量
,求质量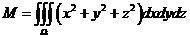 .
.
四、(14分)设函数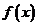 在闭区间
在闭区间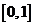 上具有连续导数,
上具有连续导数,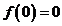 ,
, ,
,
证明: .
.
五、(14分)设函数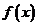 在闭区间
在闭区间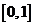 上连续,且
上连续,且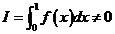 ,证明:在
,证明:在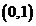 内存在不同的两点
内存在不同的两点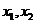 ,使得
,使得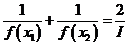 .
.
六、设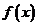 在
在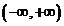 可导,且
可导,且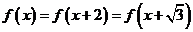 .
.
用Fourier级数理论证明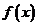 为常数.
为常数.


